[sommaire]
L’aspect fondamental de la découverte du calcul différentiel ne réside pas dans l’élaboration d’un certain nombre de règles à apprendre par cœur et à savoir utiliser. Il s’agit plutôt d’une méthode qui permet à l’individu d’appréhender la notion de changement qui régit l’univers dans lequel nous vivons : une méthode pour enseigner l’esprit de découverte. Cet aspect ayant largement été occulté depuis l’hégémonie des empiristes dans la science, nous vous invitons ici à le redécouvrir.
1. Pas de science sans poésie
Nous vivons dans un monde où rien n’est constant sauf le changement, comme Héraclite l’avait remarqué longtemps avant nous. Cependant, force est de constater que la plupart d’entre nous ont une certaine vision de notre univers comme essentiellement constitué d’objets et d’axiomes fixes interagissant les uns avec les autres. La notion de changement, ou de transformation, est ainsi plus ou moins implicitement considérée comme une sorte d’épiphénomène, si ce n’est pire ; nous baignons dans une culture de l’objet vu comme existant en soi. Pourtant, comme le montre l’histoire de la science, lorsque l’homme oublie que le changement qui engendre l’objet précède l’objet lui-même, il se condamne à ne plus rien découvrir du tout.
C’est ici que l’impact du langage sur la pensée – et donc sur la découverte – apparaît dans toute son ampleur : un véritable langage scientifique ne doit pas se borner à nommer explicitement des objets par des mots, mais doit aussi permettre d’exprimer des idées pour lesquelles les mots n’existent pas encore. Puisque la transformation est essentielle à notre univers, alors le langage de celui qui découvre devra en rendre compte.
Si l’on cherche dans l’histoire récente une période caractérisée par une explosion de découvertes fondamentales, la première place reviendra sans doute au XVIIe siècle. Cela n’a rien d’étonnant : c’est une époque au cours de laquelle le langage connaît lui-même une révolution sans précédent qui culmine avec l’invention du calcul différentiel de Leibniz en 1675. A cette époque, la science n’était pas encore séparée de la poésie comme le réclamait Hobbes dans sa guerre contre la métaphore et l’ambiguïté au nom d’une plus grande exactitude. Leibniz et ses prédécesseurs comme Pascal n’ont heureusement pas suivi cette consigne.
Comment dans un poème, une métaphore engendre t-elle une idée qui ne se trouve dans aucun des mots pris individuellement ? En associant des termes dont la juxtaposition apparaît formellement contradictoire du point de vue de l’usage habituel. Pascal cultive beaucoup ces paradoxes dans ses Pensées, mais considérons un exemple simple pris dans ses recherches scientifiques. On connaît ses célèbres expériences sur le vide : lorsqu’on retourne un tube suffisamment long et rempli de mercure, l’ouverture plongée dans un récipient plein lui-même de mercure, il subsiste dans le tube une colonne du métal qui n’atteint pas l’extrémité supérieure de ce tube. Qu’y a-t-il dans l’espace sans mercure ? Le néant ? Certainement pas : cet espace a au moins la propriété physique de laisser passer la lumière, alors que le néant n’a pas de propriété par définition. Descartes en conclut donc, par élimination, que cet espace est occupé par de la matière : feu, air, eau ou terre ; il choisit l’air et passe à côté d’une découverte majeure.
A l’opposé, comprenant qu’il y a là une nouveauté scientifique, Pascal décide d’appeler cela du vide, mais pas le vide des empiristes. Il utilise une métaphore :
Il y a autant de différence entre le néant et l’espace vide, que de l’espace vide au corps matériel. Le vide tient le milieu entre la matière et le néant.
Le vide serait donc semblable à une moyenne arithmétique ? Voilà une image pour le moins contradictoire dans les termes : il nous parle d’une entité intermédiaire entre l’être et le néant, entre rien et quelque chose, entre le zéro et la quantité… autant de « fantômes » qu’on voudrait qualifier d’ « impossibles » ou d’ « imaginaires ».
Néanmoins, il est clair que sans une telle ambiguïté dans le langage, Pascal n’aurait eu aucun moyen de communiquer et de développer sa découverte. Dès lors, on ne sera pas surpris de voir que, dans le long processus qui aboutit à la découverte du calcul différentiel par Leibniz, Pascal a joué un rôle majeur.
A la recherche d’une « caractéristique universelle »
Pour comprendre ce que signifie le calcul différentiel, il faut replacer cette découverte dans l’ensemble de la démarche intellectuelle de Leibniz, et en particulier du point de vue de sa recherche d’une « caractéristique universelle ». Cependant, précisons tout de suite qu’il y a beaucoup de confusion entretenue par différentes sectes et par les logiciens ou autres disciples de Bertrand Russell, autour de cette notion de caractéristique universelle. Pour résumer, nous dirons que ces derniers croient, ou veulent faire croire, que cette caractéristique serait une sorte de clef magique, ou une série d’axiomes, qui permettrait aux initiés de posséder toute la connaissance de l’univers. Une telle ineptie qui s’apparente plutôt aux pratiques alchimistes de Newton, se situe aux antipodes mêmes de la démarche leibnizienne. En effet pour Leibniz, aucun langage – par essence borné – ne saurait englober l’infinie transformation de notre monde. Comme Pascal, il pense qu’ici-bas seule la raison humaine, c’est-à-dire la capacité de découvrir, est capable de comprendre et de maîtriser l’univers. La caractéristique universelle ne vise pas à mettre un terme à l’interminable recherche de la vérité – tâche spécifiquement humaine ; son but est au contraire de la faciliter.
L’idée générale est de développer un langage scientifique dans lequel les mots permettraient de saisir immédiatement les propriétés des objets qu’ils désignent. A partir de là, il suffirait de connaître les règles de la grammaire permettant d’assembler ces mots, pour pouvoir remplacer par une simple phrase ce qui auparavant nécessitait un long raisonnement fastidieux. On libèrerait ainsi la pensée humaine de tout ce qui est susceptible de l’encombrer inutilement, et on lui permettrait d’aller ainsi directement à l’essentiel, c’est-à-dire à la découverte. [1]
Dans cette perspective, Leibniz s’est particulièrement attaché à développer une « caractéristique géométrique ».
A première vue, on pourrait penser qu’il a ainsi cherché à marcher sur les traces de Descartes qui avait ramené, avant lui, la description des objets de la géométrie à des équations algébriques. Il est vrai qu’on peut reconnaître immédiatement une courbe à la lecture de son équation cartésienne, etc., cependant, la géométrie cartésienne présente aux yeux de Leibniz de graves lacunes rédhibitoires. Il écrit à Huygens :
L’Algèbre n’est autre chose que la caractéristique des nombres indéterminés, ou des grandeurs. Mais elle n’exprime pas directement la situation, les angles et le mouvement.
L’approche de Descartes est très limitée. Il n’accepte dans sa géométrie que les courbes algébriques, c’est-à-dire exprimables sous la forme d’équations comprenant un nombre fini de combinaisons des quatre opérations de base (addition, soustraction, multiplication et division, les élévations à la puissance dérivant des précédentes).
Ceci met de côté toute une série de courbes dites « mécaniques » ou « transcendantes » comme la cycloïde et la chaînette – courbes pourtant étudiées par tous les géomètres de l’époque ! Descartes se condamne ainsi à ne décrire que ce qui est déjà connu, alors que pour Leibniz l’intérêt d’une caractéristique géométrique est justement de rendre accessible la nouveauté…
Plus fondamentalement, la géométrie de Descartes a le tort de s’appuyer sur les Eléments d’Euclide. Or ces Eléments nécessitent, aux yeux de Leibniz, une révision complète car ils reposent sur une série d’axiomes, de postulats et de définitions fixes présentés comme des évidences en soi et dont la nécessité n’a même jamais été discutée. Leibniz pense au contraire que la plupart des axiomes euclidiens doivent faire l’objet de démonstrations et qu’à cette fin, il faut procéder à un examen critique et systématique de toutes les définitions – considérées pourtant comme acquises par tous les géomètres depuis 2000 ans – pour en trouver de plus rigoureuses.
Qu’est-ce qu’une droite, qu’un plan, qu’un point ? On ne sait pas réellement ce que sont ces objets fixes auto-évidents sur lesquels s’appuie toute la géométrie euclidienne. Leibniz a multiplié les tentatives pour donner un sens rigoureux à ces notions, mais l’erreur serait de chercher dans ces différentes approches, des définitions au sens formel et définitif du terme. Il faut plutôt essayer d’y voir la manière dont fonctionne une pensée qui découvre.
On trouve, par exemple, dans un de ses fragments sur La caractéristique géométrique la double « définition » suivante :
Le mouvement d’un corps dont deux points demeurent immobiles offre un moyen d’engendrer la droite et le cercle ne présupposant ni l’un ni l’autre. Le mouvement de tout point de ce corps lui fera décrire un cercle, alors que tous les points immobiles se situeront sur une droite.
L’intention de Leibniz est manifeste dans ces quelques lignes : il essaie de bâtir sa géométrie non pas sur des objets abstraits donnés en soi, mais bel et bien sur une idée de mouvement ou de transformation, c’est-à-dire sur la physique elle-même. Bien entendu, il ne s’agit que d’un essai car il resterait encore à expliquer comment sont engendrés le point et le corps.
De même, dans un autre fragment, il envisage toutes les trajectoires (mouvements) qui permettent d’aller d’un point A à un point B ; il définit la droite comme la plus courte de ces trajectoires. Non seulement cette définition s’appuie, comme la précédente, sur la physique ; mais en plus, la voie est ainsi ouverte pour une physique basée sur une géométrie à courbure non nulle – voie que ne manqueront pas d’emprunter Gauss et Riemann plus d’un siècle après.
Qu’est-ce que l’« égalité » ?
Leibniz ne se contente pas simplement de redéfinir les objets de la géométrie, il entreprend de redéfinir toutes les notions. Considérons par exemple les deux propositions suivantes :
- « A est égal à B »
- « A est identique à B »
Pour la plupart de ceux qui, dans les mathématiques, privilégient l’algèbre par rapport à la géométrie, il n’y a pas de différence entre (1) et (2). Leibniz qui cherche un langage pour découvrir le monde réel n’est évidemment pas de cet avis. Il considère qu’un carré de 6 par 6 et un rectangle de 4 par 9 sont égaux, mais qu’ils ne sont pas similaires (ou semblables) ; par contre tous les carrés de toutes les tailles sont similaires entre eux. Lorsque deux objets sont à la fois égaux et similaires, il dit qu’ils sont congrus, c’est-à-dire qu’ils peuvent occuper le même lieu. Enfin, si deux objets occupent le même lieu en même temps, alors ils sont identiques.
Vue sous cet éclairage, la notion d’« égalité » ne paraît donc pas aussi évidente qu’on aurait pu le croire. Leibniz en donne alors une définition extrêmement déroutante, mais fondamentale pour le calcul différentiel :
Je juge d’ailleurs que des termes sont égaux non seulement lorsque leur différence est absolument nulle, mais aussi lorsqu’elle est incomparablement petite, et bien qu’on ne puisse dire en ce cas que cette différence soit absolument Rien, elle n’est pourtant pas une quantité comparable à celles dont elle est la différence (…) C’est précisément dans ce cas qu’on dit qu’une différence est plus petite que toute grandeur donnée .
Très étrange : deux termes sont égaux, soit si leur différence est nulle, soit si leur différence est plus petite que n’importe quelle grandeur donnée… On a l’impression que cela revient à dire deux fois la même chose. Qu’est-ce qui pourrait être plus petit que n’importe quelle grandeur donnée sinon le zéro ? Pour éclaircir ce paradoxe, Leibniz utilise un exemple pédagogique extrêmement simple (Figure 1).

Considérons un segment de droite de longueur égale à 1. Divisons ce segment par le milieu. A l’évidence, chacune des parties ainsi obtenues a une longueur égale à 1/2. Divisons à son tour le segment de droite par le milieu et joignons la moitié gauche de ce demi segment à l’autre demi segment précédent. Nous obtenons à gauche une somme de longueur égale à 1/2 + 1/4 et à droite un reste de longueur égale à 1/4. La somme ½ + 1/4 est inférieure et différente de la totalité 1. Divisons à nouveau le reste par le milieu et joignons à nouveau sa partie de gauche à la somme précédente. On obtient une nouvelle somme égale à 1/2 + 1/4 + 1/8 inférieure et différente de 1, et un nouveau reste égal à 1/8. On recommence : on obtient une nouvelle somme égale à 1/2 + 1/4 + 1/8 + 1/16 et un nouveau reste égal à 1/16. Le lecteur aura deviné qu’on peut poursuivre ce processus aussi longtemps qu’on veut : on obtient ainsi une série de sommes de plus en plus grandes, mais toujours inférieures et différentes de 1 ; et une série de restes de plus en plus petits, mais jamais nuls.
C’est ici que la question se pose : « Peut-on additionner une infinité de termes » ?
La réponse donnée par les cartésiens est bien évidemment « non » : aucun mécanisme n’est capable d’effectuer une telle opération dans notre univers ; l’expression « somme infinie » est tout simplement contradictoire dans les termes… une véritable métaphore ! Certes, ajoutera Leibniz, il est impossible d’additionner une infinité de termes, mais cette métaphore ne révèle t-elle pas une idée plus profonde que la simple idée d’addition algébrique ? En d’autres termes, peut-on donner un sens rigoureux à la notion de somme infinie ? Cette fois-ci, la réponse leibnizienne est « oui », car même si l’esprit humain n’est pas capable de concevoir individuellement chacun des termes d’une telle « somme », il peut néanmoins saisir d’un seul coup le processus qui engendre la totalité. On ne peut pas, à proprement parler, effectuer cette « somme », mais on peut constater sur cet exemple trivial que sa différence avec 1 est plus petite que toute grandeur donnée, ce qui peut s’écrire en toute rigueur :
1 = 1/2 + 1/4 + 1/8 + 1/16 + …
Le signe « = » doit donc bien se lire ici « égal à » et non pas « approximativement égal à », mais attention : n’oublions pas que, pour cela, nous avons dû transformer nos notions traditionnelles d’égalité et de somme. Il ne faut donc pas considérer l’écriture 1/2 + 1/4 + 1/8 + 1/16 + … comme un objet fixe résultant d’une somme d’objets fixes, ou comme le « dernier » terme de la série des sommes finies dont nous avons donné le début ci-dessus, mais plutôt comme un mouvement : comme le processus qui engendre la totalité de la série des sommes.
2. Tangentes et quadratures
Il serait quelque peu injuste de penser que ce n’est qu’au XVIIe siècle que l’idée de mouvement ou de transformation est devenue partie prenante de la géométrie, et qu’auparavant, cette science ne se réduisait qu’à des relations entre objets fixes, comme on serait enclin à le croire si on réduisait la géométrie grecque aux Eléments d’Euclide. Pour s’en convaincre, il faut considérer deux grands types de problèmes géométriques qui ont fait l’objet de beaucoup de recherches dans l’Antiquité, notamment de la part d’Archimède : les tangentes et les quadratures.
Tangentes
Dès la petite école, on apprend qu’ »une droite et une seule est définie par deux points distincts » et que « par un seul point passe une infinité de droites » (Figure 2).
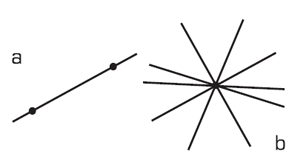
b. Par un seul point passent une infinité de droites.
Cette manière de voir se heurte néanmoins à une difficulté lorsqu’on essaie de construire la tangente à une courbe en un point donné. Considérons sur la Figure 3 le point P d’une courbe en lequel on voudrait construire la tangente. Considérons également un second point M de la courbe différent de P. On trace la droite déterminée par M et P. Ce n’est pas une tangente, mais une sécante ; elle coupe la courbe aux points P et M. Imaginons maintenant que le point M se déplace selon un mouvement continu sur la courbe en se dirigeant vers P, puis qu’il atteint et dépasse P et qu’il poursuit son chemin. A chaque nouvelle position de ce point mobile M correspond une nouvelle droite (PM). On engendre donc ainsi toute une famille de sécantes à la courbe, mais une ambiguïté survient au moment où M et P sont identiques. Que se passe-t-il alors ? Etant donné que toute droite est déterminée par deux points, faut-il croire qu’à cet instant précis, la droite cesse d’exister ou qu’il en existe au contraire une infinité ?
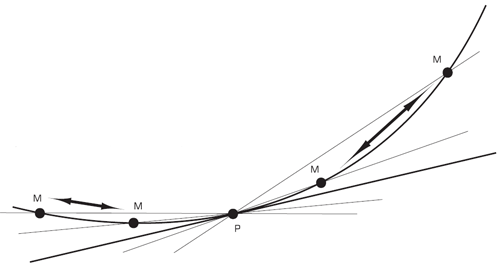
Nous devrions peut-être envisager le même problème sous un angle quelque peu différent. Considérons une sécante qui passe par le point fixe P et qui est animée d’un mouvement de rotation continu autour de celui-ci. Chacune des positions angulaires de cette sécante définit ainsi sur la courbe un point M qui va se déplacer continûment le long de celle-ci. On conçoit aisément – parce que « la nature ne fait pas de saut » (principe de continuité de Leibniz) – qu’une et une seule de ces positions angulaires correspond au cas où M et P sont identiques. A ce moment et à celui-là seulement, la sécante devient tangente. Donc la tangente en P existe et elle est unique, bien qu’il nous reste encore à déterminer quelle position angulaire lui correspond effectivement.
Voilà donc un paradoxe majeur pour ceux qui conçoivent la géométrie comme un ensemble de relations entre objets fixes : la tangente ne peut se concevoir autrement qu’engendrée par un mouvement. Ceci étant posé, il reste une question générale à résoudre : comment le géomètre peut-il pratiquement construire cette tangente ? Une droite se construisant à partir de deux points nous venons de voir que s’il existe une certaine distance entre ces deux points pris sur la courbe, on obtient une sécante qui n’est pas tangente, et que si cette distance s’annule, les deux points étant alors identiques, alors la droite est indéterminée. L’on aurait envie de dire que pour résoudre le problème dans toute sa généralité, il nous faudrait disposer de deux points dont la distance ne serait ni nulle, ni une certaine quantité ! Nous voici donc à la recherche d’un être hybride, intermédiaire entre le zéro et la quantité.
En utilisant des artifices sur des cas particuliers, les Grecs ont su construire des tangentes pour beaucoup de courbes. Ils purent ainsi démontrer assez facilement que la tangente en un point situé sur la circonférence d’un cercle est la perpendiculaire au rayon qui passe par ce point. Cependant, ils n’ont pas trouvé de méthode générale pour toutes les courbes. C’est Leibniz qui résolut le problème par la découverte du calcul différentiel.
Quadratures
Un autre des grands problèmes de la géométrie classique est celui des quadratures, c’est-à-dire notamment le calcul des surfaces délimitées par des courbes (et le calcul des volumes délimités par des surfaces). Qu’est-ce qu’une surface ? Dans quelle mesure peut-on dire que deux surfaces sont égales ou que l’une est supérieure à l’autre ? Ces questions ne sont pas évidentes en soi. Leibniz propose que deux objets sont égaux si en modifiant l’arrangement des parties de l’un, il devient congru à l’autre (c’est ainsi qu’un rectangle de 9 par 4 est égal à un carré de 6 par 6). Il ajoute qu’un objet est inférieur à un autre s’il est égal à une partie de ce dernier. C’est en se basant sur de tels principes qu’on peut chercher à comparer des surfaces de formes très diverses, en prenant par exemple un certain carré comme unité.
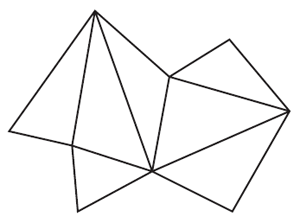
Les Grecs ont montré qu’un rectangle étant donné, on peut trouver un carré qui lui soit égal ; qu’un triangle est égal à la moitié d’un rectangle ; et qu’un polygone quelconque peut être décomposé en une somme finie de triangles (Figure 4).
Il en résulte que, pour tout polygone donné, on sait trouver le carré qui lui soit égal ; d’où l’origine du mot quadrature.
La question se pose ensuite : peut-on réaliser la quadrature d’une surface délimitée par une ou plusieurs lignes courbes ?
Cherchons par exemple S, la surface délimitée par la courbe OB et les deux droites perpendiculaires OA et AB de la Figure 5. Divisons par exemple la droite horizontale OA en un certain nombre d’intervalles égaux et construisons deux séries de rectangles à partir de la courbe et de cette division.
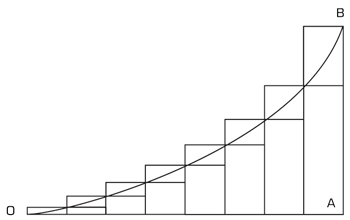
Appelons I la série de rectangles inscrits dans la courbe et C la série de rectangles circonscrits sur la courbe. Selon la définition de l’inégalité proposée ci-dessus, il vient immédiatement deux relations :
S > I et S < C.
On ne sait pas déterminer S à priori, mais l’on sait déterminer C et I.
Considérons également R, le dernier rectangle de la série C. La largeur de R est égale au pas de la division de OA, et sa hauteur est égale à la valeur maximale de la courbe. Sa surface est évidemment le produit des deux. Il vient également :
R = C - I.
Recommençons la même construction avec un pas de la division deux fois plus court que précédemment. Nous aurons deux fois plus de divisions de OA qu’auparavant, et deux nouvelles séries, C1 et I1, ainsi qu’un nouveau rectangle R1.
On constate que : S > I1 > I , S < C1 < C et R1 < R.
Nous pouvons continuer ce processus aussi longtemps que nous voulons. Or la série R1, R2, R3… peut être rendue aussi petite que n’importe quelle quantité donnée ; par conséquent la différence entre la grandeur engendrée par la série des I et la grandeur engendrée par la série des C est plus petite que n’importe quelle quantité donnée. Donc ces deux grandeurs sont égales et leur valeur commune est précisément la valeur S recherchée qu’il nous reste à calculer pratiquement. On voit au passage, comme pour la tangente, que la quadrature ne résulte pas d’une relation statique entre objets, mais qu’elle est engendrée par une certaine transformation. S « ordonne » (ou transcende) les deux séries I et C sans faire partie ni de l’une, ni de l’autre.
Cependant, nous nous heurtons ici à un paradoxe similaire à celui que nous avons rencontré ci-dessus. Tant que la largeur de la division de OA est égale à une certaine quantité, les deux séries de rectangles ne donnent pas la valeur exacte de S ; par contre, si la largeur de cette division était nulle, on aboutirait à une impossibilité de « remplir » la surface S car les rectangles seraient alors des segments de droite dont la surface est nulle. Donc, ici encore, il nous faut trouver, pour la largeur de la division, un être étrange qui puisse tenir le milieu entre le zéro et la quantité.
Ici encore, en utilisant des artifices particuliers, les géomètres de l’Antiquité, comme Archimède, ont su calculer des quadratures pour un certain nombre de courbes. Par exemple, si la courbe de la Figure 5 est une parabole, la portion sous la courbe vaut un tiers du rectangle dont les côtés sont OA et OB. Cependant, ils n’ont pas trouvé de méthode générale (en particulier Archimède s’est acharné, en vain, à réaliser la « quadrature du cercle »). Ce problème général trouve une solution dans le calcul intégral de Leibniz.
3. Deux problèmes réciproques
On utilise souvent l’expression « calcul différentiel » pour désigner le calcul différentiel et le calcul intégral. En réalité ces deux calculs sont réciproques l’un de l’autre bien que cette propriété ne saute pas immédiatement aux yeux lorsqu’on commence à s’interroger sur les tangentes et les quadratures, même si à ce stade de cet article, on peut percevoir que pour calculer une tangente, il faut effectuer une « différence » et que pour calculer une quadrature il faut effectuer une « somme ». Cependant, une étape décisive fut franchie par Leibniz dans ses recherches sur le sujet, lorsqu’il étudia le célèbre triangle arithmétique ou triangle de Pascal.

Nous avons représenté ce triangle sur la Figure 6. Voici son principe de construction. Il s’agit d’un tableau qui comporte une infinité de lignes et de colonnes numérotées 1, 2, 3, 4… On place tout d’abord un nombre dans la case de la première ligne et de la première colonne, 1 par exemple. On dispose ensuite le même nombre 1 dans toutes les cases de la première ligne et toutes les cases de la première colonne. On utilise ensuite une règle unique pour remplir toutes les autres cases : dans chaque case, on place un nombre égal à la somme du nombre qui se trouve immédiatement au-dessus de lui et du nombre qui se trouve immédiatement à sa gauche.
Ceci étant posé on voit apparaître sur la seconde ligne en partant du haut, la suite des nombres entiers : 1, 2, 3, 4, 5, 6… La troisième ligne donne la suite des nombres dits « triangulaires » : 1, 3, 6, 10, 15, 21… La quatrième ligne donne la suite des nombres dits « pyramidaux » : 1, 4, 10, 20, 35, 56… La cinquième ligne donne la suite : 1, 5, 15, 35, 70, 126… etc. Avec un peu de réflexion, on découvre un certain nombre de propriétés remarquables de ce triangle comme sa symétrie par rapport à la diagonale : les mêmes suites de nombres qu’on place dans les différentes lignes se retrouvent intégralement dans les colonnes correspondantes.

Etudions ces différentes séries de nombres et leurs relations réciproques. Pourquoi, par exemple, la troisième série porte-t-elle le nom de « triangulaire » et la quatrième le nom de « pyramidale » ? La réponse se trouve sur la Figure 7, où nous avons représenté une sorte de réseau de points se trouvant sur les sommets de triangles équilatéraux. Si l’on considère les deux premières lignes de ce réseau, nous voyons un triangle constitué de 3 points ; si l’on considère les trois premières lignes, nous voyons un triangle de 6 points ; si l’on considère les quatre premières lignes nous voyons un triangle de 10 points ; et ainsi de suite. On construit de la sorte toute la série des nombres triangulaires. Notons avant de poursuivre, que sur chaque ligne de ce réseau, se trouve un certain nombre de points correspondant à un élément de la suite des nombres entiers (c’est-à-dire la seconde ligne du triangle de Pascal).
Ceci étant énoncé, il sera facile pour le lecteur de se représenter la suite des nombres pyramidaux, non pas sur un plan comme la série triangulaire, mais dans un espace à trois dimension. On dispose donc un point sur la première couche, un triangle de 3 points sur la seconde couche, un triangle de 6 points sur la troisième couche, un triangle de 10 points sur la quatrième couche, etc., et l’on voit apparaître une pyramide à 1 point, une pyramide à 4 points, une pyramide à 10 points, une pyramide à 20 points, et ainsi de suite. On construit donc ainsi la série pyramidale, en constatant au passage que, par construction, chaque couche de cette série de pyramides nous donne un nombre de la série triangulaire.
Ces relations réciproques observées entre les quatre premières lignes du triangle de Pascal se généralisent à toutes les séries de nombres suivantes. Il existe une harmonie parfaite dans ce tableau entre les principes qui ordonnent les nombres sur chacune des séries, et les principes qui ordonnent les différentes séries entre elles. Le triangle de Pascal représente une série ordonnée de séries. Comment passe-t-on d’une ligne à la suivante, et d’une ligne à la précédente, dans le cas général ? En fait, il est facile de démontrer que chaque nombre se trouvant à l’intersection d’une certaine ligne et d’une certaine colonne est égal à la somme de tous les nombres de la ligne (ou de la colonne) précédente, depuis le premier jusqu’à celui qui se trouve exactement au-dessus (à gauche) de lui.
Pour démontrer cela, il suffit simplement de partir du principe de construction du triangle – chaque nombre est égal à la somme de celui qui est au-dessus de lui et de celui qui est à gauche de lui – d’appliquer ce principe à celui de gauche, et encore à celui de gauche, etc. Donc par simple lecture, chaque nombre du tableau correspond immédiatement à une somme. On peut généraliser encore cette remarque si on s’intéresse à des sommes tronquées, c’est-à-dire des sommes de nombres consécutifs dont le premier n’est pas nécessairement sur la première colonne (ou la première ligne) du tableau. Si l’on veut calculer la somme de tous les nombres d’une certaine ligne du rang i au rang j (avec i < j), on voit sans trop de difficulté que quelle que soit la longueur d’une telle somme, elle est simplement égale à la différence de deux termes situés sur la ligne suivante : le terme de rang j auquel on enlève le terme de rang i - 1. Par exemple, sur la cinquième et la sixième ligne, il apparaît immédiatement que 15 + 35 + 70 + 126 = 252 - 6. La différence de deux termes est évidemment plus rapide à calculer que la somme d’un grand nombre de termes.
En résumé, chaque suite, ou progression, donne les différences de la suite suivante et les sommes de la ligne précédente. L’opération qui permet de passer d’une ligne à la précédente est donc la différentiation, et l’opération réciproque est la sommation. Le lecteur peut s’amuser à effectuer des différentiations successives d’autres progressions, comme la série des carrés 1, 4, 9, 16, 25, 36…, la série des cubes 1, 8, 27, 64, 125… et voir ce qui en découle. Il se rendra compte, par exemple, que la série des carrés est de la même espèce que celle des nombres triangulaires.
Du triangle arithmétique au triangle harmonique
Lors de son séjour à Paris entre 1672 et 1676, le jeune Leibniz découvrit les travaux de Pascal (décédé depuis 1662) grâce à Huygens. Dans son ouvrage Quadrature arithmétique du cercle, de l’ellipse et de l’hyperbole, qui n’a été publié qu’à la fin du XXe siècle, Leibniz montre l’importance pour ses propres découvertes, des travaux de Pascal. Inspiré par le triangle arithmétique, il conçut lui-même un « triangle harmonique » obtenu en inversant les nombres du précédent (on remplace 1 par lui-même, 2 par 1/2, 3 par 1/3, 4 par 1/4…). Ce nouveau triangle permet également de différentier et de sommer des séries de nombres, d’une manière assez semblable à celle de Pascal, mais la nouveauté ici, est que l’on peut également calculer toute une série de sommes infinies, ainsi :
1/1 + 1/2 + 1/3 + 1/4 + 1/5 + ... = 1/0 (infini)
1/1 + 1/3 + 1/6 + /1/10 + /1/15 + ... = 2/1
1/1 + 1/4 + /1/10 + /1/20 + /1/35 + ... = 3/2
1/1 + 1/5 + /1/15 + /1/35 + /1/70 + ... = 4/3 etc.
Mais laissons à Leibniz le soin de nous donner ses démonstrations :
« Soit A la série 1/1 + 1/2 + 1/3 + 1/4 etc.
« Soit 2/1 B la série 1/1 + 1/3 + 1/6 + 1/10 etc.
« La série 1/2 + 1/6 + 1/12 + 1/20 etc. sera égale à B.
« Soustrayons termes à termes la série B de la série A, restera A-B,
si par exemple de 1 on ôte 1/2 restera 1/2 ; si de 1/2 on ôte 1/6 restera 1/3.
« Si de 1/3 on ôte 1/12 restera 1/4.
« Et de même, dans la suite, les termes de la série A réapparaîtront toujours dans l’ordre qui est le leur, on pourrait le démontrer en toute généralité (…)
« La série 1/2 + 1/3 + 1/4 + 1/5 etc. sera par conséquent égale à A-B.
« Or cette même série 1/2 + 1/3 + 1/4 + 1/5 etc. est aussi égale à A-1.
« On obtient donc une égalité entre A-B et A-1, soit entre B et 1, soit encore entre 2B et 2. 2B soit encore 1/1 + 1/3 + 1/6 + 1/10 etc. sera donc égal à 2. CQFD ».
Les autres sommes infinies se calculent d’une manière analogue.
4. Le problème de Kepler
Au XVIIe siècle, toute la communauté scientifique est à la recherche d’une nouvelle méthode pour calculer les tangentes et les quadratures. Il nous faut cependant préciser ici ce qui, 1800 ans après la mort d’Archimède, a décidé tout ce monde à se mettre à l’ouvrage.
L’aiguillon intellectuel vient de Kepler qui publie son Astronomie nouvelle, en 1609. A cette époque le débat fait rage pour savoir si la Terre tourne autour du Soleil ou si c’est le contraire. Cependant, malgré certaines idées reçues, ce n’est pas exactement là que se situe le véritable enjeu scientifique du moment. Kepler ne cherche pas simplement à déterminer quel est le mouvement des astres, mais surtout quelle est la cause physique de ce mouvement. C’est en cela qu’il est unique dans la science de son temps.
Depuis Aristote, les astronomes considèrent que le mouvement des astres est nécessairement circulaire uniforme, ou composé d’un certain nombre de mouvements circulaires uniformes. Ils cherchent donc un modèle mathématique, c’est-à-dire la combinaison de mouvements circulaires uniformes qui permet de « coller » au mieux aux observations. Or, si l’on observe les planètes, on constate que celles-ci donnent l’impression d’accélérer, de ralentir, voire de repartir en arrière, au cours de leur voyage.
Pour certains comme Galilée ou Copernic, cette irrégularité n’est qu’une apparence qui s’expliquerait par le fait que nous sommes nous-mêmes entraînés par le mouvement de la Terre. Ainsi, nous aurions l’impression que les planètes ont parfois un mouvement rétrograde à la manière dont nous avons l’impression dans un train d’être immobiles et que le paysage recule.
Kepler ne se satisfait pas de cette réponse. Il pense que la Terre est effectivement en mouvement autour du Soleil comme les autres planètes qui donnent ainsi l’apparence de rétrogradations ; mais qu’il y a également une irrégularité réelle, et pas simplement observée, dans tous ces mouvements. Il pense que la force qui meut les planètes se situe dans le Soleil : lorsque la planète se rapproche du Soleil, elle accélère ; lorsqu’elle s’éloigne, elle ralentit.

Quand l’arc de trajectoire est court la vitesse est petite et quand l’arc de trajectoire est long la vitesse est grande.
Dans sa révolution autour de l’étoile, la planète voit donc sa vitesse varier en permanence entre deux extrêmes : un maximum atteint au périhélie (le point de la trajectoire le plus proche du Soleil) et un minimum atteint à l’aphélie (le point le plus éloigné). Ces remarques conduisent Kepler à faire l’hypothèse que si l’on considère la surface balayée par le rayon géométrique qui relie la planète au Soleil pendant une certaine portion du déplacement, cette surface est proportionnelle à la durée correspondante.
On peut voir sur la Figure 8 que plus la planète est proche du Soleil, plus elle est rapide, de manière à pouvoir conserver l’égalité des aires pour des durées égales.
Cependant, l’irrégularité du mouvement n’aurait aucune raison d’être physique si la planète se déplaçait sur un cercle dont le Soleil serait au centre. Kepler suppose donc dans un premier temps que le mouvement est circulaire mais que le Soleil n’est pas au centre ; il se trouverait à une distance fixe du centre, l’excentrique.
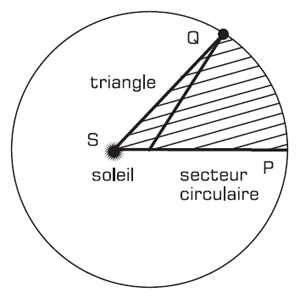
Si l’on considère, comme sur la Figure 9, qu’on connaît deux positions de la planète P et Q distinctes, alors on pourra facilement en déduire le temps nécessaire pour aller de l’une à l’autre. En effet, si on connaît les deux positions extrêmes de la planète (périhélie et aphélie), on connaît le diamètre du cercle complet et, par conséquent sa surface totale qui est balayée en une année. Donc si on connaît la surface balayée entre P et Q, on pourra donc en déduire, par proportionnalité, le temps mis pour aller de P à Q. Or, ici cette surface est très facile à calculer : il suffit de remarquer qu’elle peut se décomposer en un secteur circulaire et un triangle, que l’on sait déterminer séparément. Donc si l’on connaît le chemin parcouru par la planète, on saura donc calculer le temps de ce parcours.
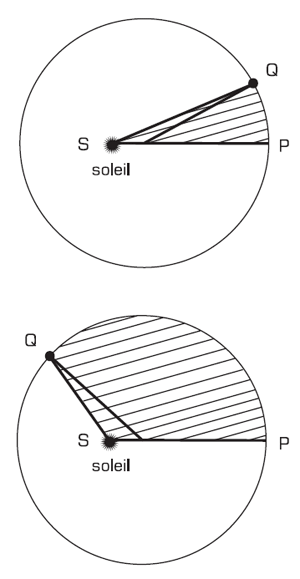
Cependant, c’est le problème inverse qui intéresse le plus l’astronomie : pour faire des prévisions astronomiques, il faut savoir dire où se trouvera la planète pour un instant futur donné. Donc, comment calculer le chemin parcouru pendant un temps donné ? On se convaincra aisément que ce problème est bien plus ardu que le précédent. Ayant la donnée du temps, nous avons la valeur algébrique de la surface balayée pendant ce temps. Comment passer de la donnée de cette valeur qui ne nous renseigne pas directement sur la forme géométrique de la surface, à la longueur correspondante de l’arc de trajectoire recherché, sans laquelle on ne connaît pas la surface ? Pour deux durées différentes, nous avons deux surfaces de formes très différentes (Figure 10) ; il n’y a pas de relation géométrique simple entre l’arc et la surface comme ce serait le cas par exemple avec un secteur circulaire (avec le Soleil au centre) pour lequel l’arc et la surface sont proportionnels.
Ne trouvant pas de solution générale, Kepler utilisa une méthode d’approximation qui consistait à diviser le périmètre du cercle en 360 arcs égaux et à calculer toutes les surfaces balayées correspondantes. Ayant ainsi établi une correspondance entre 360 positions de la planète et 360 surfaces (donc 360 durées) il put, se donnant a priori une durée, déterminer une approximation de la position. Une telle démarche n’est évidemment qu’un pis-aller, car dans chacun de ces arcs, le mouvement de la planète change une infinité de fois et l’on ne peut pas extrapoler linéairement la position pour une durée intermédiaire, à moins de calculer toutes les positions pour toutes les durées possibles ce qui est évidemment impossible. Un arc d’une longueur non nulle enveloppe une infinité de « moments de changement » ; et un arc de longueur nulle, si on peut parler d’une telle chimère, n’enveloppe rien du tout. D’une manière similaire à ce que nous avons vu ci-dessus au sujet du problème de la tangente, nous sommes confrontés à la difficulté d’isoler un « moment de changement » entre le zéro et la quantité. Conscient et insatisfait de l’imperfection de sa méthode, Kepler comprit que la détermination de mouvements irréguliers nécessitait une nouvelle géométrie qui n’existait pas encore. C’est ainsi qu’il lança un appel à tous les géomètres dans son Astronomie Nouvelle, pour que ce problème soit résolu.
Signalons tout de même que sa « mauvaise » méthode ne fut pas inutile : l’appliquant à l’orbite de Mars, il découvrit qu’elle ne donnait pas des prévisions conformes aux mesures. Cherchant la part d’arbitraire dans ses hypothèses, il comprit qu’il n’avait aucune raison physique de présupposer la trajectoire circulaire et de placer le Soleil sur un point arbitraire distinct du centre. Il était par contre plus légitime de placer le Soleil au foyer d’une ellipse. C’est ainsi qu’il découvrit que les trajectoires des planètes sont elliptiques.
5. La méthode de Fermat
Comme on le voit avec Kepler, toute la difficulté de la recherche scientifique consiste à trouver des causes physiques invisibles dont on ne constate que des effets interreliés les uns avec les autres et qui ne cessent jamais de varier. La seule méthode efficace consiste à faire des hypothèses sur les raisons de ces changements et à les confronter avec l’expérience pour les valider ou les infirmer.
Il faut préciser que lorsqu’on étudie un phénomène qui varie en permanence, certains moments singuliers ont une importance capitale parce qu’ils caractérisent le plus directement les causes physiques qu’on recherche. Parmi ces moments singuliers figurent de manière primordiale les extremums, c’est-à-dire les minimums et les maximums. Par exemple, comme on le voit en astronomie dans l’Harmonie du monde de Kepler, le périhélie et l’aphélie de la trajectoire d’une planète, qui correspondent aux valeurs maximale et minimale de sa vitesse, sont des caractéristiques majeures de l’ensemble du mouvement. C’est souvent sur la mesure de tels extremums que l’expérimentateur va tester la validité de son hypothèse. On comprendra donc que l’une des premières tâches d’une méthode de calcul dont le but est de rendre compte du changement, sera la détermination des minimums et des maximums représentatifs de ce changement.
Ces considérations de physique expérimentale qui soulignent l’importance de la recherche d’extremums sont cependant transcendées par une raison métaphysique plus profonde. Cette raison s’exprime par le « principe de moindre action » de Leibniz, mais elle était connue avant lui sous d’autres formes moins évoluées. Voici comment se résume le raisonnement. A moins d’abandonner la science pour le bénéfice de la magie, nous sommes contraints de reconnaître qu’il ne se produit rien dans notre univers qui n’ait de raison suffisante pour son existence. En conséquence, si plusieurs voies s’offrent à la nature pour produire un certain effet général, c’est celle qui minimise l’action qui sera effectivement mise en oeuvre, sinon une partie de l’action utilisée l’aura été en pure perte (à moins que cette action produise un autre effet que celui dont il est question, mais ce n’est justement pas le cas envisagé ici). Un tel « gaspillage » serait donc sans raison. En conséquence, la transformation générale que l’univers exerce sur lui-même, est soumise au principe de moindre action.
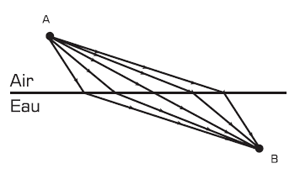
Dans le cas particulier des recherches de Fermat sur l’optique, ceci se traduit par le principe selon lequel, pour se rendre d’un point A à un point B la lumière emprunte le trajet qui minimise le temps mis en œuvre, étant donné que la lumière est d’autant plus rapide que le milieu de propagation est moins dense (Figure 11).
Fermat, un autre des précurseurs importants de Leibniz, avait compris que la recherche des minimums et des maximums s’apparente, en géométrie, à la détermination des tangentes. Il se dota donc d’une nouvelle manière de représenter les objets de la géométrie.
Considérons par exemple une courbe dans un plan. Fermat cherche à caractériser le mouvement qui l’engendre. Il choisit une droite dans le plan et un point O sur cette droite (Figure 12).
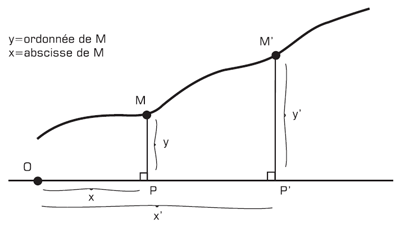
Il projette ensuite chaque point M de la courbe sur cette droite, par exemple par une projection orthogonale. La hauteur du segment ainsi tracé, reliant M à P s’appelle ordonnée. On peut la désigner par y. La distance sur la droite entre P et O s’appelle abscisse. On peut la désigner par x. On voit donc que le mouvement du point M qui engendre la courbe est ramené à deux mouvements interreliés d’extension (ou de contraction) de l’abscisse et de l’ordonnée. La relation algébrique, entre ces deux mouvements, qui caractérise la courbe elle-même s’appelle « équation ». Une telle courbe peut donc décrire un phénomène de transformation physique qui s’exprime par l’interaction de deux grandeurs.
Ne pensez pas à une telle représentation dans les termes de ce que l’on présente à l’école sous le nom de « coordonnées cartésiennes », même si, d’un point de vue algébrique, cela semble la même chose. Pour comprendre la nuance, rappelez-vous que vous avez pris l’habitude, comme par réflexe, de placer sur une feuille de papier deux (ou trois) axes orthogonaux avant même de tracer quoi que ce soit d’autre. Une telle habitude reflète un certain préjugé répandu dans la physique : on suppose, sans vraiment s’en rendre compte, que l’espace est absolu, c’est-à-dire qu’il existe un certain environnement neutre, immuable, une sorte de décor arbitrairement donné dans lequel les évènements ont lieu (et dans lequel le temps s’écoule de manière uniforme). Or ceci ne correspond pas à la réalité physique, comme on le savait bien avant la relativité : l’espace (ainsi que le temps) est partie prenante de l’action qui s’y produit. Il est très significatif à ce sujet que lorsqu’ils représentent un problème géométrique physique, Fermat, Pascal, Leibniz et ceux qui leur sont associés, décrivent d’abord les courbes et ensuite les axes sur lesquels ils les projettent (préfigurant en quelque sorte les recherches de Gauss sur comment mesurer la courbure d’un univers dont celui qui mesure fait lui-même partie). C’est le parti que nous avons pris délibérément ci-dessus.
Dans le système à coordonnées cartésiennes où l’espace est donné a priori comme absolu indépendamment de l’action, les différents axes sont, en particulier, indépendants les uns des autres. Un tel a priori embarrasse l’esprit pour saisir l’idée de variété à plusieurs dimensions connexes. Cette idée riemannienne était déjà implicite, avant Descartes, dans les travaux astronomiques de Kepler.
A cela, il faut ajouter que le point de vue de Fermat privilégie le mouvement qui engendre la courbe : celle-ci n’est donc pas vue comme une collection statique de points, comme nous avons trop pris l’habitude de le penser. En fait, une droite, ou plus généralement une courbe, n’est pas à proprement parler, un ensemble dont les parties seraient des points statiques : un point est une frontière, pas une partie.
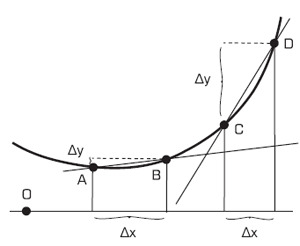
Considérons maintenant un second point de la courbe, M’. Il est associé à sa projection, P’, son ordonnée, y’ et son abscisse, x’. M et M’ définissent une sécante à la courbe. Cette dernière est elle-même caractérisée par deux différences : la différence des ordonnées Δy = y’ - y, et la différence des abscisses : Δx = x’ - x (ou encore y’ = y + Δy et x’ = x + Δx).
Ce ne sont pas ces différences qui vont nous permettre d’étudier la transformation de la courbe, mais plutôt leur rapport Δy/Δx. Ce dernier est d’autant plus grand que Δy est grand et que Δx est petit.
On le constate aisément sur la Figure 13 : entre A et B, Δx est relativement grand et Δy relativement petit, donc leur rapport est relativement petit ; entre C et D c’est le contraire.
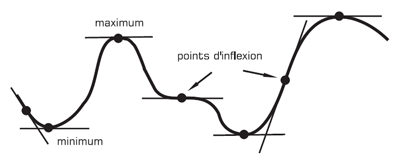
A quoi cela correspond-il en termes géométriques ? La croissance de la courbe est plus « lente » entre A et B et plus « rapide » entre C et D. Cependant, il n’est pas correct de parler de croissance entre deux points distincts qui définissent une sécante car, comme on l’aura compris, cette croissance varie une infinité de fois entre ces deux moments. C’est pourquoi, la sécante n’est pas le meilleur moyen d’étudier la croissance d’une courbe. Pour cela, il est préférable de construire des tangentes. La tangente est un reflet des « moments de changement » de la courbe : plus la tangente est inclinée, plus la croissance de la courbe est importante ; inversement, lorsque la tangente est « horizontale », la croissance de la courbe est minimale – en fait nulle (Figure 14). Or, dans quelles circonstances la tangente est-elle horizontale ? Le plus souvent, lorsque la courbe atteint un minimum ou un maximum.
A partir de sa méthode pour représenter les courbes dont il disposait avant que Descartes ait publié quoi que ce soit sur le sujet, Fermat développa donc un calcul pour construire les tangentes et déterminer les extremums des courbes. Cette méthode a très directement inspiré le calcul différentiel de Leibniz qui en constitue une généralisation. Il faut toutefois noter ici une remarque importante de Leibniz au sujet des minimums et des maximums : ces points singuliers sont totalement dépendants du choix arbitraire des abscisses et des ordonnées.
Dans ses propres travaux, Leibniz n’hésite d’ailleurs pas, à plusieurs reprises, à remplacer les abscisses par les ordonnées et vice-versa. En d’autres termes, bien qu’ils soient d’une importance capitale, les extremums ne sont pas des caractéristiques intrinsèques à la courbe. La véritable caractéristique de la courbe, qui ne dépend pas du choix des axes, c’est sa courbure. Sur notre exemple, on voit que celle-ci change de sens pour certains points singuliers qu’on appelle points d’inflexion. Ces points présentent la particularité d’avoir une tangente qui traverse la courbe.
6. Entre l’être et le néant : le devenir
Pourquoi l’idée de trouver un intermédiaire entre le zéro et la quantité, plus petit que toute quantité donnée, nous semble t-elle tellement choquante ? La réponse réside, bien entendu, dans notre habitude de concevoir le monde comme une collection d’objets. Ainsi nous voyons la courbe comme un certain alignement de points « élémentaires ». Chassons ce préjugé en comprenant que seul le changement est véritablement élémentaire, et le paradoxe qui nous embarrasse se dissipera comme par enchantement. Fort de cette résolution, Leibniz (et Fermat avant lui) inventa donc de nouvelles règles algébriques pour donner aux moments de changement, un véritable droit de reconnaissance. Il leur donna donc le nom de « différentielles » pour les distinguer des « différences » dont il a été question ci-dessus. On les appelle aussi « quantités infiniment petites » ou « quantités infinitésimales » pour donner des expressions faciles à retenir, mais il ne faut pas perdre de vue que ce ne sont pas de véritables « quantités » au sens habituel du terme.
Si l’on considère une variable algébrique quelconque, par exemple l’abscisse ou l’ordonnée d’une courbe x ou y, on lui associe une différentielle que l’on nomme en accolant le préfixe « d » au nom de la variable, ce qui donne dx ou dy. Cette différentielle est un nouveau type de variable : c’est le moment de changement de la variable à laquelle elle est associée. Dans le cas d’une courbe décrite par le changement continu d’une abscisse et d’une ordonnée, le moment de changement de la courbe est associé à deux moments de changement : celui de l’abscisse et celui de l’ordonnée. Si maintenant on compare la quantité x et la quantité x + dx, c’est-à-dire si l’on soustrait l’un à l’autre, on obtient dx qui est, par définition, plus petit que toute quantité donnée. En conséquence, d’après la définition de l’égalité donnée par Leibniz, on peut écrire en toute rigueur, et au grand scandale de tous les algébristes :
x = x + dx
bien que dx ne soit généralement pas nul.
Répétons-le : ceci n’est vrai que parce que dx n’est pas une véritable quantité comme le serait une différence telle que celle que nous avons désignée ci-dessus par Δx. Avec une véritable différence, nous aurions dû écrire x ≈ x + Δx, c’est-à-dire non pas une véritable égalité, mais une approximation. Mais l’exemple d’une découverte de Fermat réécrite avec la notation de Leibniz devrait rendre l’intérêt de tout ceci plus facile à saisir.
Tangente d’une parabole
Dans le système de Fermat, une courbe est exprimée par une relation algébrique générale qui lie l’abscisse et l’ordonnée de chacun de ses points. Un exemple simple est celui de la courbe dont l’abscisse prend successivement les valeurs de tous les nombres possibles tandis que l’ordonnée prend les valeurs des carrés de ces nombres.
| x | -2 | -1 | 0 | 0,5 | 1 | 1,5 | 2 | 3 | 4 | 5 | 10 |
| y | 4 | 1 | 0 | 0,25 | 1 | 2,25 | 4 | 9 | 16 | 25 | 100 |
Cette courbe est une parabole, et elle s’exprime par l’équation suivante :
Y = x2 (1)

Question : considérons une tangente en un point quelconque de la parabole (Figure 15) : en quel point coupe-t-elle l’axe de symétrie ?
Réponse : d’après ce qui précède, la distance entre le point M de coordonnées x et y, et le point de coordonnées x + dx et y + dy, est plus petite que toute quantité donnée. Ces deux points sont donc sur la parabole, ce qu’on peut dire autrement en affirmant qu’on peut remplacer x et y dans l’équation de la parabole respectivement par x + dx et y + dy. On dit qu’on différentie l’équation (1). Il vient :
y + dy = (x+dx)2 (2)

Pour les mêmes raisons, ces deux points se trouvent tous les deux sur la tangente à la parabole. Cette tangente fait donc apparaître deux triangles rectangles semblables. Le premier a un côté égal à x et un autre égal à une certaine longueur IP recherchée qui se trouve entre le point I d’intersection de la tangente et de l’axe de symétrie d’une part, et la projection orthogonale P de M sur l’axe de symétrie d’autre part. Les côtés du second triangle sont les différentielles dx et dy. Nous les avons représentés sur la figure bien qu’en réalité ils soient impossibles à dessiner. Il y a donc similitude (proportionnalité) entre le « grand » triangle, et le « triangle différentiel » (qui n’est pas un triangle au sens habituel du terme).
Que signifie le membre de droite de l’égalité (2) ? Il signifie « le carré de côté x + dx », que l’on représente de manière approximative (car dx est en réalité plus petit que toute quantité donnée donc impossible à dessiner) par la Figure 16. On voit apparaître quatre parties dans ce carré : un carré de côté x, deux « rectangles » de côtés x et dx, et un « carré » de côté dx.
D’où :
(x + dx) 2 = x2 + 2x.dx + (dx)2 (3)
Avec (2) et (3), nous obtenons :
y + dy = x2 + 2x.dx + (dx)2 (4)
Si de chaque côté d’une égalité, on enlève la même quantité, on obtient une nouvelle égalité. En enlevant (1) à (4) membre à membre, on obtient donc :
dy = 2x.dx + (dx)2 (5)
Considérons maintenant le membre de droite de cette dernière égalité. Nous avons vu qu’il désigne deux rectangles et un carré qui ont tous les trois un côté dx. On peut donc les disposer de manière à ce qu’ils forment un rectangle dont l’un des cotés est x + x + dx et l’autre dx. On obtient donc une autre manière d’écrire (5) :
dy=(x + x + dx)dx (6)
Or, comme x = x + dx, il vient finalement l’équation différentielle suivante :
dy = (x + x)dx = 2x.dx
donc : dy = 2x.dx (7)
ou encore : dy/dx = 2x
Or, cette équation nous donne la relation de proportionnalité entre les deux côtés du « triangle différentiel » qui est lui-même similaire au « grand » triangle comme nous l’avons remarqué plus haut. Nous avons donc :
IP/x = dy/dx = 2x
donc : IP/x = 2x
donc : IP = 2x2 = 2y d’après (1)
Pour finir IP = 2y
Or si l’on considère le sommet de la parabole, O, on a OP = y.
IP = 2y entraîne donc OI = y.
O est au centre du segment délimité par P et I. Dit autrement, l’intersection I de la tangente en M et de l’axe de symétrie de la parabole se trouve donc être le symétrique de la projection P de M par rapport au sommet de la parabole.
On en déduit une méthode pour tracer la tangente en un point M quelconque d’une parabole : il suffit de projeter M sur l’axe de symétrie de la courbe et de placer le point I symétrique de cette projection par rapport au sommet. La tangente est la droite déterminée par les deux points M et I.
Pour garder notre même exemple de la parabole, intéressons-nous maintenant au cas particulier du sommet de la courbe, c’est-à-dire ici, le point pour lequel l’abscisse et l’ordonnée sont toutes les deux égales à zéro. Compte tenu de notre choix arbitraire des axes de projection de la courbe, nous avons en ce sommet un minimum pour la courbe (c’est-à-dire que l’ordonnée y est minimale) et, comme il se doit, une tangente « horizontale » en ce point. Or comment cette situation s’exprime t-elle en termes algébriques ? Si nous reprenons l’équation différentielle écrite ci-dessus, nous avons dy = 2xdx. Au point O l’abscisse x est nulle, donc, en ce point particulier le moment de changement dy est lui-même nul : dy = 0. C’est ainsi que le calcul différentiel est utilisé pratiquement pour déterminer les extremums des courbes : on cherche à partir de l’équation différentielle, les points pour lesquels le moment de changement de l’ordonnée s’annule (ici dy = 0). Dans le cas de notre parabole, la solution à ce problème est immédiate et unique : c’est le sommet, le point d’intersection de la courbe avec l’axe de symétrie.
Cependant, si nous avions décidé de représenter la parabole autrement, par exemple en permutant le rôle de l’abscisse et de l’ordonnée, nous n’aurions trouvé aucun extremum. En effet, x jouant le rôle de l’ordonnée et y celui de l’abscisse, (1) devient :
x = √y
donc (7) s’écrit : dy=2√ydx
ou encore dx = dy/2√y
Aucune valeur de y ne permet d’annuler dx, donc cette courbe n’a pas d’extremum pour l’ordonnée x.
Nova methodus
En 1684, Leibniz publia dans Acta Eruditorum un article en latin dont le titre traduit en Français est : Nouvelle méthode pour chercher les minima et les maxima, ainsi que les tangentes, méthode que n’entravent pas les expressions fractionnaires ou irrationnelles, accompagnée du calcul original qui s’y applique. C’est dans cet article qu’il présenta pour la première fois la notation de son calcul différentiel, les règles de calcul et des exemples d’application. Destiné à prendre date, cet article extrêmement sec ne donne aucune démonstration des principes du nouveau calcul. Néanmoins, le lecteur au fait des recherches de l’époque sur le sujet, pouvait théoriquement remonter aux principes par lui-même. Ce ne fut malheureusement pas toujours le cas.
Nous avons choisi dans l’exemple précédent de la parabole, un problème concernant l’interaction de deux grandeurs, pouvant donc donner lieu à une représentation géométrique simple dans le plan. Le calcul différentiel s’applique en réalité à un nombre quelconque de variables. Dans un premier temps, Leibniz s’applique à exprimer des règles algébriques trouvées avant lui par différents géomètres sous d’autres formes, mais en utilisant sa propre notation qui permet d’en faire la synthèse. Ce ne sont donc pas ces règles en soi qui constituent véritablement la découverte de Leibniz, mais plutôt la notation elle-même car, comme nous le verrons plus loin, celle-ci met en évidence des paradoxes insolubles du point de vue de la géométrie algébrique de Descartes, et nécessite une révolution conceptuelle.
Commençons donc par donner un aperçu des règles de différentiation. Désignons par x, y, z des quantités variables et A une quantité considérée constante. Comme on l’a vu sur l’exemple précédent, pour différentier une expression faisant intervenir plusieurs variables x, y, z… on remplace ces dernières par x + dx, y + dy, z + dz… Compte tenu de ce qui précède, il n’est pas trop difficile d’établir ce qui suit.
- La différentielle d’une constante est nulle : dA = 0. Ceci n’a rien d’étonnant puisque par définition une constante ne change pas.
- Différentielle d’une multiplication : d(xy) = xdy + ydx. Pour s’en convaincre, il suffit de s’inspirer de la différentiation du carré de côté x que nous avons effectuée ci-dessus, en l’appliquant à un rectangle de côtés x et y.
En particulier si l’un des deux côtés est constant, il vient : d(Ax) = Adx (car dA = 0).
D’autre part, on généralise cette règle pour une multiplication de plus de deux termes, en remarquant que xyz = (xy)z (la multiplication de trois termes est ainsi ramenée à un multiplication de deux termes…) Il suit de cela :
d(xyz) = xydz + zd(xy) = etc.
- La différentielle d’une somme est égale à la somme des différentielles : d(x + y + z) = dx + dy + dz.
- Différentielle d’une inversion.
Posons y = 1/x. et cherchons dy c’est-à-dire d(1/x). Pour cela il faut remarquer que xy = 1 et différentier cette expression. Il vient xdy + ydx = d(1) = 0 (car 1 est une constante).
Donc xdy = -ydx ou encore :
dy = -(y/x)dx.
Si l’on remplace y par sa valeur, on obtient finalement : d(1/x) = -dx/x2
- Sachant différentier une multiplication et une inversion, on sait différentier une division puisque la division x/y peut s’écrire sous la forme de la multiplication x.(1/y).
Donc si z = x/y,
alors dz = (ydx-xdy)/y2
- Différentiation d’une élévation à la puissance.
Dans l’exemple de la parabole, nous avons différentié une élévation au carré :
Si y = x2, alors dy = 2xdx.
Sachant différentier un produit, nous pouvons généraliser cette relation. Il vient :
Si y = x3, alors dy = 3x2dx
Si y = x4, alors dy = 4x3dx
Si y = x5, alors dy = 5x4dx
Si y = x6, alors dy = 6x5dx
…Plus généralement, si y = xn,
alors dy = n.x(n-1)dx, si l’exposant n désigne un nombre entier.Cependant, Leibniz remarque que cette écriture peut même se généraliser à des exposants non entiers. Sachant qu’on peut écrire x-1 = 1/x, x-2 = 1/x2… ainsi que √x = x1/2… on retrouve ainsi les expressions de d(1/x) et d(√x) que nous avions établies précédemment.
S’inspirant encore de notre différentiation précédente de la parabole, nous pouvons dès lors nous amuser à construire de manière similaire les tangentes pour toutes les courbes à degrés entiers y = x3, y = x4… Remarquons toutefois que lorsque nous différentions l’une de ces courbes pour construire ses tangentes, nous faisons apparaître l’expression de la courbe de degré précédent à un facteur multiplicatif près (par exemple, on construit les tangentes de la courbe d’ordonnée y = x5 avec la courbe d’ordonnée z = 5x4…). Nous pouvons différentier cette nouvelle expression pour obtenir une expression de degré inférieur, et ainsi de suite. En effectuant ainsi ces différentiations successives, nous établissons ainsi des relations entre différentes courbes, exactement comme nous avions établi précédemment des relations entre différentes séries de nombres dans le triangle arithmétique et le triangle harmonique.
Descartes, rappelons-le, ne tolérait dans sa géométrie que des courbes dites algébriques. Les règles de différentiation données par Leibniz permettent de manière exhaustive de construire les tangentes pour toutes ces courbes. De plus, comme nous venons de le constater, la différentiation de l’expression d’une courbe algébrique, fournit l’expression d’une nouvelle courbe algébrique. Donc la construction des tangentes ne pose pas un problème majeur pour la géométrie cartésienne, et le fait est que les géomètres du XVIIe siècle savaient les construire pour toutes les courbes algébriques, avec leurs méthodes propres, avant même Leibniz, bien que la notation de celui-ci ait constitué une simplification considérable dans les calculs. Quel est, dans ce cas, l’apport révolutionnaire de Leibniz ?
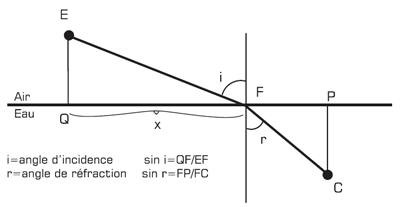
Avant d’aborder cette question fondamentale, disons quelques mots sur le premier exemple d’application choisi par Leibniz pour illustrer l’intérêt de sa méthode, dans son article Nova methodus. La Figure 17 représente la trajectoire d’un rayon lumineux entre un point E situé dans un milieu peu dense (l’air par exemple) et un point C dans un milieu plus dense (l’eau). Comment cette trajectoire est-elle déterminée ? Prenant le parti de Fermat et de Huygens contre Descartes (et également contre Newton), Leibniz considère que ce trajet est celui qui minimise le temps par lequel la lumière passe de E en C, et que la lumière est d’autant plus rapide que le milieu est moins dense (la lumière est plus rapide dans l’air que dans l’eau). Ceci étant posé, la trajectoire qui est égale à la somme des segments EF et FC, ne sera connue que lorsque la position de F sera connue – tous les autres lieux du problème E, Q, P et C étant donnés a priori. Leibniz désigne par r la densité de l’air et par h la densité de l’eau.
La vitesse de la lumière dans un milieu étant inversement proportionnelle à la densité du milieu, Leibniz désigne par 1/r la vitesse de la lumière dans l’air et par 1/h la vitesse de la lumière dans l’eau. Si la lumière a une vitesse constante entre E et F alors cette vitesse sera égale à la distance EF divisée par le temps pour aller de E à F. Ce temps est donc égal à EF divisé par la vitesse, c’est-à-dire à EF multiplié par la densité r. En raisonnant de la même manière pour calculer le temps mis dans l’eau, on en déduit le temps total w pour aller de E en C : w = EF.r + FC.h. Leibniz appelle x = QF la variable qui permet d’exprimer la position de F. Toutes les autres distances se calculent à partir de cette seule variable (FP = QP - x ; EF2 = EQ2 + x2 …). On peut donc imaginer une courbe d’ordonnée w et d’abscisse x, et chercher la valeur de x pour laquelle w serait minimale, c’est-à-dire pour laquelle dw = 0. Il en découle, après calcul de l’expression de dw – et sans avoir besoin de tracer effectivement cette courbe – que la position de F (la valeur de x) est telle, que le rapport des sinus des angles incident et réfracté est égal au rapport (constant) des vitesses de la lumière dans les deux milieux. En quelques lignes de calcul, Leibniz retrouve donc la fameuse loi des sinus établie par Snell et Fermat.
Le problème inverse des tangentes engendre une anomalie
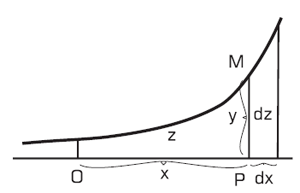
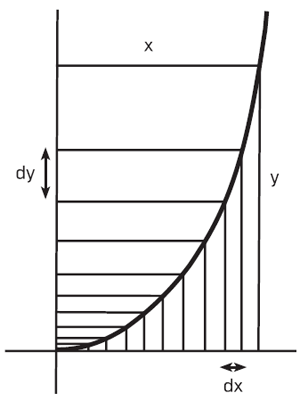
Nous avons vu précédemment, qu’une courbe étant donnée, nous pouvons construire ses tangentes en établissant l’expression d’une nouvelle courbe obtenue par l’opération de différentiation. La question qui nous intéresse ici est de savoir si, une courbe étant donnée, il existe une également expression permettant de calculer toutes les surfaces qu’elle délimite. Considérons donc la Figure 18. Nous avons une surface z délimitée par une certaine courbe, par l’axe des abscisses et par les ordonnées en deux points O et P. Le point O est choisi arbitrairement fixe ; le point P donne l’abscisse x = OP d’un point M qui décrit la courbe et dont l’ordonnée est y = PM. Le point M est donc déterminé par les deux variables x et y ; à chacune de ses positions correspond une surface z. Le problème que nous nous posons ici est donc de construire la courbe d’abscisse x et d’ordonnée z (qui exprime donc toutes les surfaces pour toutes les positions de M). On peut remarquer, pour commencer, qu’on connaît immédiatement un point de cette courbe : lorsque x=0, nous avons z=0 (la surface est alors nulle).
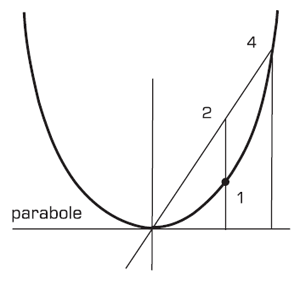
Pour se fixer les idées, le lecteur peut par exemple considérer la courbe d’équation y = 2x. Il s’agit en fait d’une droite (Figure 19). Pour chacune des valeurs de x, il est donc facile de calculer la surface z correspondante puisqu’il s’agit de la surface d’un triangle. Le lecteur n’aura pas trop de difficulté à se rendre compte que z = x2. Il apparaît donc que la courbe d’abscisse x et d’ordonnée z est précisément la parabole que nous avions différentiée ci-dessus.
Laissons là cet exemple, et retournons au cas général. Nous cherchons une courbe dont l’ordonnée z est déterminée par la surface de la courbe initiale d’ordonnée y = PM. Que se passe-t-il si l’on cherche à différentier z ? Il apparaît que dz est un « rectangle différentiel » dont l’un des côtés est la différentielle dx et l’autre coté, la longueur y :
dz = y.dx
En effet, nous avons vu précédemment – bien que ce terme soit ici impropre – que la quadrature est une « somme infinie » de quantités différentielles ; z est obtenu par la somme infinie de tous les rectangles y.dx. Donc il apparaît bel et bien ici, que le calcul des surfaces est le calcul réciproque de celui des tangentes. Pour l’exprimer, Leibniz utilise le symbole « ∫ » qu’on appelle somme ou « intégrale », et donne le nom d’« intégration » à cette nouvelle opération.
Il note ici : z = ∫ydx. Cette notation étant établie, peut-on comme dans le cas du calcul différentiel établir des règles de calcul ? On peut commencer par inverser les relations précédentes. En les reprenant avec les mêmes conventions, nous pouvons écrire :
∫dx = x
∫Aydx = A∫ydx
∫(y + z)dx = ∫ydx + ∫zdx
xy = ∫ydx + ∫xdy (Figure 20)
Nous pouvions différentier n’importe quelle expression algébrique. En est-il de même pour l’intégration ? Voyons ce qui se passe pour la simple question de l’élévation à la puissance. Nous avions établi précédemment :
dxn = n.x(n-1)dx.
Il semble apparemment facile d’inverser cette relation comme nous l’avons fait avec la droite et la parabole. Nous obtenons :
∫dxn = ∫n.x(n-1)dx, d’où :
xn = n . ∫x(n-1)dx,
ce qui s’écrit encore :
xn/n=∫x(n-1)dx
Donc il semblerait que l’on sache intégrer n’importe quelle élévation à la puissance par la formule :
∫x(n-1)dx = xn/n
Par exemple : ∫xdx = x2/2 (c’est une variante de notre exemple de la parabole)
∫x2dx = x3/3
∫x3dx = x4/4…
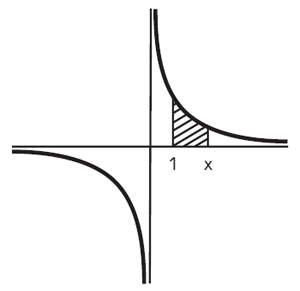
Mais attention : il y a une anomalie ! Le membre de droite n’est pas calculable pour n=0. Quelle est la signification d’une telle singularité quant à la quadrature que nous cherchons à exprimer ? Nous avons déjà dit que x-1 est une autre manière d’écrire 1/x ; il y a donc ici une difficulté pour calculer ∫(1/x)dx, donc pour calculer la quadrature de la courbe d’équation y = 1/x. Or cette courbe est connue des géomètres, il s’agit d’une hyperbole (Figure 21). [2]
Faut-il donc renoncer à calculer cette quadrature pour la raison que la formule algébrique générale est impossible à calculer dans ce cas particulier, alors qu’une simple représentation graphique de l’hyperbole force notre raison à admettre l’existence d’une telle quadrature ? La réponse de Descartes à une telle question est indiscutablement « oui ». Que répondra Leibniz ? L’impossibilité d’utiliser la formule algébrique ne prouve pas que la quadrature de l’hyperbole n’existe pas, mais simplement qu’elle ne peut pas s’exprimer par une formule algébrique ! Il nous faut donc renoncer à une géométrie qui ne tolèrerait que des courbes algébriques pour éviter de tomber dans des paradoxes ridicules. Comme Leibniz l’a montré dans sa Quadrature arithmétique du cercle, le problème de la quadrature de l’hyperbole est du même type que celui de la quadrature du cercle : dans les deux cas, il est nécessaire de faire intervenir une « somme infinie » (non algébrique) pour l’exprimer.
Bien que la quadrature de l’hyperbole soit « impossible » à calculer d’un point de vue algébrique, il serait manifestement absurde de prétendre qu’elle n’existe pas. La courbe qui permet de construire cette quadrature n’est pas algébrique, elle est dite « transcendante ». En fait, elle fait partie d’une famille de courbes connues depuis longtemps des géomètres, du fait de leurs propriétés caractéristiques, sous le nom de « logarithmes ». La principale particularité de ces courbes est que si l’on prend comme abscisses une suite géométrique de nombres, les ordonnées correspondantes formeront une suite arithmétique (ou le contraire, pour les courbes réciproques des logarithmes que l’on appelle aujourd’hui « exponentielles »). On a par exemple dans le logarithme à base 10, la correspondance suivante :
| Abscisses | 0,001 | 0,01 | 0,1 | 1 | 10 | 100 | 1000 | 10 000 |
|---|---|---|---|---|---|---|---|---|
| Ordonnées | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
(la raison de la suite géométrique des abscisses est ici 10, et la raison de la suite arithmétique des ordonnées est 1).
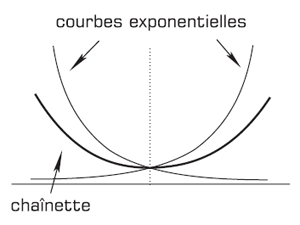
Ces logarithmes (exponentielles) jouent un rôle fondamental dans la physique : grâce au calcul différentiel, Leibniz et Bernoulli sont parvenus séparément à déterminer la courbe décrite par une chaînette suspendue entre ses deux extrémités. Cette chaînette est en réalité la moyenne arithmétique de deux exponentielles, l’une étant obtenue à partir de l’autre en lui faisant effectuer une rotation d’un demi-tour autour de l’axe des ordonnées (Figure 22).
Commettant le même type d’erreur que Descartes, Galilée avait cherché quel type de courbe algébrique pourrait le plus « coller » à la chaînette, et il avait conclu que la chaînette était une parabole. Bien que l’erreur de Galilée fût connue depuis longtemps, un nouveau calcul, ou plutôt une nouvelle manière de penser était nécessaire pour déterminer la véritable nature de la chaînette. La manière correcte, c’est-à-dire plutôt « physique » que « mathématique » de déterminer cette courbe, consiste en fait à exprimer une caractéristique de la gravitation : « Soit une chaînette dont la longueur et les deux extrémités sont données, quelle est la forme qui minimise la hauteur de son centre de gravité ? »
Ainsi on peut dire que le calcul différentiel/intégral a donné leurs « droits civiques » aux courbes transcendantes dont les logarithmes ne sont qu’un premier exemple.
7. Les fluxions entravent la pensée
Le calcul des fluxions (= vitesses) de Newton n’est qu’une mauvaise caricature du véritable calcul différentiel. Cependant, le fait qu’aujourd’hui encore, l’on croie que Leibniz et Newton ont fait tous les deux la même invention de manière indépendante, montre la confusion d’idées qui règne dans les esprits des scientifiques. Ces derniers semblent comme conditionnés à ne pas comprendre la différence entre les deux calculs. Officiellement, ils sont équivalents, et ne diffèrent que par leurs notations respectives. L’argument utilisé pour justifier cette affirmation est qu’on peut traduire les règles de l’un dans le langage de l’autre et réciproquement. C’est ici qu’il faut chercher à voir au-delà des apparences du formalisme mathématique, car ces règles algébriques ne sont qu’un reflet de la découverte, mais pas la découverte elle-même.
Le fait est que le calcul des fluxions réclame de telles contorsions intellectuelles, qu’il n’a jamais véritablement été utilisé. A ce sujet, il n’est pas inutile de signaler qu’au moment de la polémique sur l’antériorité de l’invention, Bernoulli avait fait remarquer à Leibniz que Newton commettait des erreurs sur des problèmes concernant des différentiations successives, ce qui semblait montrer que sa notation ne lui permettait pas de maîtriser cette question essentielle. Ceci donna l’idée à Leibniz de tester les newtoniens en leur proposant un certain nombre de problèmes que son calcul permettait de résoudre – une initiative qui emplit Newton de fureur…
C’est sans doute Lazare Carnot, dans ses Réflexions sur la métaphysique du calcul infinitésimal, qui exprime le mieux au XVIIIe siècle la différence entre le calcul différentiel et le calcul des fluxions, et qui montre, dans un langage certes diplomatique, la raison majeure de la supériorité du premier sur le second :
Les procédés de la méthode des fluxions ne diffèrent de ceux de l’analyse infinitésimale que par la notation. Au lieu de la caractéristique d, dont on se sert dans celle-ci, on pointe les lettres dans la méthode des fluxions, c’est-à-dire que la fluxion de la variable ou fluente x, par exemple, est représentée par x′, mais avec cette distinction, que x′ représente une quantité finie qui est la vitesse du point décrivant dans le sens des abscisses, tandis que dx, dans le calcul différentiel, représente une quantité infiniment petite, qui est l’accroissement instantané de cette même abscisse.
En d’autres termes, Leibniz a révolutionné l’algèbre en y introduisant l’idée de changement par l’usage des différentielles, alors que Newton a ramené l’algèbre dans son état antérieur en faisant disparaître cette idée par un tour de passe-passe pour n’y laisser subsister que celle de quantité. On impose ainsi aux esprits l’idée d’un monde composé d’une collection d’objets, par opposition à un monde gouverné par la transformation. Une telle vision est tout à fait cohérente à la philosophie de l’école empiriste dont Newton est un représentant majeur.
Comment procède-t-il ? Reprenons notre exemple de la tangente à la parabole. Nous avions établi une relation de proportionnalité entre un triangle au sens habituel du terme, et un « triangle différentiel » dont les côtés ne sont pas des longueurs mais des différentielles. Nous avons pu écrire cette relation grâce à une équation différentielle que nous venions d’établir :
dy = 2x.dx
Les deux termes de cette équation sont différentiels. Cependant, nous avons montré que ceci pouvait également s’écrire : dy/dx = 2x Le premier terme de cette équation est un rapport de deux différentielles, mais ce rapport est lui-même une quantité et non pas une différentielle. Cette quantité représente également le rapport entre les deux côtés du triangle « normal ». On voit donc que si l’on divise tous les termes différentiels d’une équation par un même terme différentiel, on obtient une équation algébriquement équivalente mais qui ne fait intervenir plus que des quantités finies. Par exemple, considérons la relation suivante :
5xt + 3y – y2t + 6t2 - 13 = 0
On obtient par différentiation une nouvelle équation :
5x.dt + 5t.dx + 3dy - 2yt.dy – y2dt + 12t.dt = 0
Tous les termes de cette équation sont des éléments différentiels. Si l’on divise tout par dt, il vient :
5x + 5t(dx/dt) + 3(dy/dt) - 2yt(dy/dt) – y2 + 12t = 0
Algébriquement, cette dernière équation est équivalente à la précédente, bien qu’elle ne fasse intervenir que des quantités finies. Newton écrit en fait x′ pour dx/dt, y′ pour dy/dt… ce qui donne :
5x + 5t x′ + 3y′ - 2yty′ – y2 + 12t = 0
Voilà comment toutes les règles du calcul ont été réécrites. Toute référence à ce « moment de changement », à mi-chemin entre l’être et le néant, qui constitue le véritable fondement du calcul différentiel, a disparu.
Ceci n’a été possible que parce qu’on a attribué, de manière tout à fait arbitraire, un rôle privilégié à l’une des variables, t, par rapport à toutes les autres. Cette variable qui sert en quelque sorte de référence absolue, est donc supposée, selon les propres termes de Newton dans La méthode des fluxions et des suites infinies, « augmenter par une fluxion uniforme » (c’est le mot « uniforme » qui est important ici). Il est très significatif que Newton ait décidé d’appeler cette variable « le temps » pour fixer les idées de son lecteur : il pense que le temps (ainsi que l’espace) est absolu. Cette question a donné lieu à une violente polémique dans la Correspondance Leibniz Clarke (Clarke représentant le point de vue de Newton). Le calcul de Newton repose donc intrinsèquement sur une vision fausse de la physique d’un temps et d’un espace absolus. Néanmoins, ce point de vue erroné a été imposé et a constitué, jusqu’à ce jour, un sérieux handicap pour la physique, en dépit des découvertes ayant conduit à la relativité.
A la fin du XVIIIe siècle, Carnot et Monge ont dispensé un enseignement leibnizien dans la science française, et en particulier à l’Ecole Polytechnique, mais après 1815, ils furent chassés et remplacés par Cauchy qui dénatura, d’une manière similaire à Newton, l’esprit du calcul différentiel par son usage des « limites » qui constitue aujourd’hui encore la base de l’enseignement du calcul dans les écoles. Une révolution dans l’enseignement pour restaurer l’esprit de découverte est plus que jamais nécessaire.
Sur la question des définitions
Il est dangereux de trop se fixer sur la définition formelle des concepts, plutôt que de chercher à voir comment l’esprit qui découvre parvient à saisir ces concepts : on finit par confondre mentalement le concept et la définition et bloquer le développement d’idées nouvelles. A titre d’exemple, il peut être utile de se demander ce qu’est réellement un nombre premier. A une telle question, chacun est habitué à débiter comme par réflexe : « Un nombre premier est un nombre dont les seuls diviseurs sont 1 et lui-même ».
Oui, et alors ? En quoi cette définition arbitraire nous apprend-elle l’importance de la notion de nombre premier ? Dans l’enseignement actuel, on n’apprend l’importance de cette notion qu’après avoir appris la définition par cœur, ce qui n’est pas naturel car ce n’est pas ainsi qu’un esprit fait des découvertes.
Que signifie le mot « premier » dans l’expression « nombre premier » ? Pourquoi avoir donné un tel nom à cette notion ? La réponse se trouve dans une certaine idée selon laquelle ces nombres « précèdent » ou « engendrent » en quelque sorte tous les autres. Celui qui a énoncé le premier l’expression « nombre premier » a donc donné ainsi une trace de ses recherches sur l’idée de « nombre » : il ne considérait pas les nombres comme des entités auto-évidentes à manipuler sans les connaître, mais cherchait à comprendre leur véritable nature et la manière dont ils sont créés. De telles interrogations sont à l’origine de percées scientifiques majeures comme la découverte du domaine complexe par Gauss.
Ainsi, lorsque nous disons qu’un nombre premier n’est divisible que par 1 et par lui-même, nous ne devrions pas prendre cette proposition comme une définition et nous en tenir là, mais simplement comme une propriété qui n’est peut-être pas la plus fondamentale.
Le projet Newton contre le projet Leibniz
Dans son ouvrage How The Nation Was Won, l’historien américain H. Graham Lowry montre comment Leibniz a joué un rôle clef dans un immense projet politique visant à établir une nouvelle forme de gouvernement républicain opposée à la logique d’empire héritée de Venise. De ce projet est notamment issue la révolution américaine. Bien qu’il ne soit pas possible de résumer ici ce travail, il est néanmoins nécessaire d’en donner quelques points de repère pour comprendre la véritable signification de la polémique sur le calcul différentiel.
Les guerres de religion du XVIe et du XVIIe siècle manipulées par Venise dans un but de « diviser pour régner » ont dévasté toute l’Europe. A la naissance de Leibniz, la Guerre de trente ans (1618-1648) est sur le point de s’achever grâce aux efforts de la diplomatie de Mazarin et l’établissement du Traité de Westphalie. De nombreux humanistes à travers le monde s’organisent en réseaux non seulement pour reconstruire l’Europe, mais surtout pour développer une véritable culture républicaine. Ils partagent la vision selon laquelle chaque homme possède une capacité d’invention et de découverte qui, si elle est éduquée et développée en société, peut servir l’intérêt général et améliorer la condition humaine. Cette vision est, bien entendu, opposée à la logique d’empire selon laquelle une oligarchie doit asservir et « bestialiser » le reste de l’espèce humaine.
Profitant de troubles internes en Angleterre, un groupe d’humanistes autour de John Winthrop réussit à obtenir dès 1630 une charte pour établir une colonie dans la baie du Massachusetts dans des conditions de grande autonomie. Grâce à son éloignement, cette colonie constituera un véritable « laboratoire de gouvernement républicain » dont l’un des piliers sera l’éducation pour tous. Les descendants de John Winthrop poursuivront l’oeuvre du fondateur contre les efforts de l’empire britannique visant à détruire cette dynamique. John Winthrop Jr. sera l’un des innombrables correspondants de Leibniz dans les réseaux républicains en Amérique et en Europe.
En France, l’homme de confiance de Mazarin, Jean Baptiste Colbert, crée à Paris l’Académie des sciences, dont le but est de rassembler des savants du monde entier pour organiser un processus social de découverte. Les quatre années, de 1672 à 1676, passées à Paris sont décisives pour la formation et les découvertes du jeune Leibniz. Convaincu que l’homme doit être libéré de ses tâches physiques, par l’invention de machines, afin d’avoir plus de temps pour penser et découvrir, Leibniz n’a de cesse de gagner le plus de monde possible à son idéal républicain. Leibniz est ainsi l’ennemi absolu de toute forme d’esclavagisme. Il est notamment à l’origine de plusieurs académies inspirées de celle de Colbert, dont celles de Berlin et de Moscou. Il gagne également le soutien de nombreux décideurs politiques dont le Tsar Pierre le Grand, et la duchesse Sophie de Hanovre pressentie pour être la future reine d’Angleterre.
Une telle influence ne pouvait que paniquer le « parti vénitien » qui a progressivement pris le contrôle idéologique de la Grande-Bretagne, d’autant plus que Leibniz attaquait l’un des principaux propagandistes de l’Empire britannique, John Locke. Ce dernier, que l’on présente à tort comme un inspirateur d’idées républicaines, est un grand bénéficiaire du colonialisme britannique ; il a notamment rédigé la constitution de la Caroline par laquelle est codifié un esclavage particulièrement brutal. Est-ce contradictoire avec sa Lettre sur la Tolérance ? Pas du tout : les citoyens sont égaux devant la loi, mais la citoyenneté s’acquiert selon lui par la propriété. Un homme qui ne possède rien, pas même sa liberté, n’est donc pas un citoyen.
Dans son Essai sur l’entendement humain, Locke précise que les idées nous viennent par nos sens et qu’il n’existe pas d’idée innée. C’est précisément ce point que Leibniz dénonce comme une fraude dans ses Nouveaux essais sur l’entendement humain car s’il n’y a pas d’idée innée, il n’y a pas de morale universelle : le bien et le mal ne sont que des conventions arbitraires. Si l’on convainc la société d’accepter une telle conséquence, il devient possible de s’opposer à l’esclavage dans les pays « civilisés » et de le préconiser chez les « sauvages », donc de maintenir un empire tyrannique par des moyens plus « efficaces » qu’une monarchie absolue…
Comment alors ruiner la réputation et la dangereuse influence politique de Leibniz ? En créant le mythe du génie universel de Newton. Isaac Newton est une figure clef de l’empire britannique. Ami de Locke, sa fortune est considérable. Au début du XVIIIe siècle, il dirige la Royal Society, l’Académie des sciences d’Angleterre. Cette dernière est utilisée comme outil de contrôle social : principale caisse de résonance de l’empirisme dans la science, elle permet à l’Empire de garder le contrôle des inventions susceptibles de révolutionner le monde (c’est ainsi que l’inventeur Denis Papin disparut en Angleterre avec les plans de sa machine à vapeur capable de naviguer).
En 1712, la Royal Society instruisit un procès pour « prouver » que non seulement Leibniz n’avait pas découvert le calcul différentiel, mais qu’il avait plagié cette découverte dont le mérite reviendrait à Newton lui-même. Faut-il préciser que les conclusions de l’enquête de la Royal Society furent favorable à son directeur ? Pourtant, à y regarder de près, cette histoire ne tient pas un seul instant. Leibniz a sans arrêt enrichi son calcul de découvertes nouvelles comme l’atteste la quantité invraisemblable d’articles et de publications de sa part. Newton aurait, selon la légende, découvert le calcul, mais n’aurait jamais rien publié à ce sujet pendant plus de 20 ans, et n’aurait pas fait croître sa progéniture… Comme il était manifestement impossible de nier à Leibniz sa capacité de découverte, on inventa un autre mensonge plus subtil, mais qui parvint à subsister jusqu’à aujourd’hui. Selon ce nouveau conte, Leibniz et Newton auraient chacun inventé le calcul différentiel indépendamment l’un de l’autre ; Newton aurait simplement précédé Leibniz d’une dizaine d’années.
Ayant calomnié Leibniz sur le terrain mathématique, les empiristes purent ensuite lancer une attaque générale contre ses idées philosophiques lesquelles sont à la base de ses projets politiques. La Correspondance Leibniz-Clarke représente en quelque sorte le coup d’envoi de cet assaut lancé dans les derniers mois de la vie de Leibniz. En Europe, cette attaque sera relayée tout au long du XVIIIe siècle par les empiristes britanniques et les Lumières françaises (Fontenelle, Voltaire, Maupertuis, Buffon, Diderot, d’Alembert…). A l’écart de cette propagande, les héritiers de Leibniz en Amérique, dont Benjamin Franklin, créeront la première république de l’histoire moderne.
Bibliographie
- Carnot L., Réflexions sur la métaphysique du calcul infinitésimal, Paris, Blanchard, 1970.
- Cauchy A., Le calcul infinitésimal, Paris, ACL-éditions, 1897.
- Descartes R., La géométrie, J. Gabay, 1991.
- Kepler J., Astronomie nouvelle, traduit par J. Peyroux, Paris, Blanchard, 1979.
- Leibniz G.W., Naissance du calcul différentiel, 26 articles des Acta Eruditorum, texte introduit, traduit et annoté par M. Parmentier, Paris, Vrin, 1989.
- Leibniz G.W., La caractéristique géométrique, texte établi, introduit et annoté par J. Echeverria, traduit annoté et postfacé par M. Parmentier, Paris, Vrin, 1995.
- Leibniz G.W., Quadrature arithmétique du cercle, de l’ellipse et de l’hyperbole, texte introduit, traduit et annoté par M. Parmentier, Paris, Vrin, 2004.
- Correspondance Leibniz Clarke, présentée par A. Robinet, Presses Universitaires de France, 1991.
- Newton I., La méthode des fluxions et des suites infinies, traduit par Buffon, Paris, Blanchard, 1994.
- Pascal B., Œuvres complètes, introduit et annoté par L. Lafuma, Paris, Seuil, 1963.

